Н.В. Семенов, А.Н. Труфанов, Н.А. Труфанов
Пермский национальный исследовательский политехнический университет, Пермь, Россия 2013

Исследовано влияние реальной геометрии формы профиля сечения заготовки легированного кварцевого силового стержня для анизотропного оптического волокна «Panda» на характер поля остаточных напряжений, формирующихся при изготовлении стержня. Решена краевая задача нестационарной теплопроводности и по найденному распределению температур решена краевая квазистатическая задача об остаточных напряжениях в заготовке силового стержня.
Проведено сравнение результатов, полученных при осесимметричной постановке с идеально круглой формой сечения, с результатами плоской задачи, где учитывалась реальная форма геометрии.

Выявлено, что некруглость профиля сечения приводит к несимметричности и локальным концентрациям полей остаточных напряжений по сечению, что может являться причиной разрушения заготовок. Наблюдаются существенные изменения величин, которые считаются важными при исследовании прочности. Разница между наименьшим и наибольшим значениями максимальных главных касательных напряжений на границе оптических сред между легированным кварцевым стеклом и чистым кварцем растет при увеличении отклонения от круглой формы сечения.

Ключевые слова: остаточные напряжения, стеклование, кварцевое оптоволокно.

Введение

Среди различных типов светопроводящих оптических волокон существует класс специальных (анизотропных) волокон, поддерживающих поляризацию светового сигнала и применяемых, например, для изготовления чувствительных элементов волоконно-оптических гироскопов [1–3]. К данному классу световодов относится волокно типа Panda. Его главной конструктивной особенностью заготовки является наличие двух цилиндрических легированных кварцевых стержней, которые устанавливаются так, что центры стержней расположены симметрично на одной линии с центром светопроводящей жилы. Такие стержни называют силовыми. Изготавливают их модифицированным методом химического осаждения из газовой фазы (MCVD) [4], который заключается в том, что при высокой температуре происходит осаждение на внутренней поверхности опорной кварцевой трубки слоев кварца, легированного оксидом бора, после чего трубка схлапывается и остывает. Такие стержни устанавливаются в подготовленные заранее отверстия в заготовке, затем ее размягчают под действием высокой
температуры и вытягивают в волокно. В вытянутом волокне после охлаждения возникают внутренние напряжения. Остаточное напряженное состояние анизотропного световода определяется совокупностью факторов, связанных со свойствами материалов и условиями технологического процесса изготовления: неоднородностью температурных полей, несовместностью температурных деформаций неоднородно легированных элементов, терморелаксационными переходами (стеклование–размягчение), происходящими из-за неоднородного легирования в различных температурных диапазонах. Основная цель введения в конструкцию световода силовых стержней заключается в создании в поперечном сечении светопроводящей жилы максимальной разности главных напряжений. Чем она больше, тем больше величина модового двулучепреломления, являющегося одной из ключевых характеристик анизотропного оптического волокна.

Заготовка силового стержня для анизотропного волокна типа Panda представляет собой круглый цилиндр длиной (l) 0,5 мм и радиусом (r2) ≈ 5 мм, изготовленный из кварцевого стекла, легированного оксидом бора В₂О₃ с зависящей от радиуса концентрацией µ(r) . Исследование технологических процессов, проходящих при изготовлении заготовок стержней и самих волокон обычно ведется с использованием предположения о том, что сечения представляют собой идеальные окружности [5–8], однако на практике профиль сечения зависит от множества факторов, как случайных, так и определенных технологией изготовления. С целью определения реальной геометрии зоны легирования в силовых стержнях были исследованы более ста образцов. Анализ полученных данных показал, что граница легированной зоны Г в реальных заготовках силовых стержней по тем или иным причинам получается некруговой формы. Типичная картина отклонения легированной зоны от круга приведена на рис. 1.

 

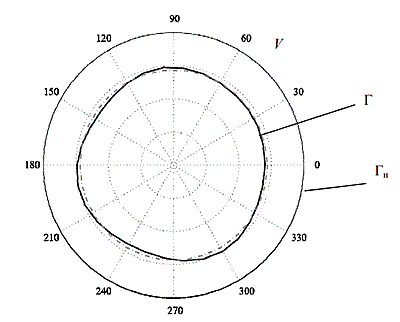
Рис. 1. Диаграмма зависимости R(φ) в полярной системе координат для одного типичного стержня:
Г – граница между легированной сердцевиной и кварцевой оболочкой;
Гн – наружная граница заготовки

Другим важным результатом анализа является установление факта, что большинство исследованных стержней имеет схожую по характеру и близкую по абсолютным значениям отклонения закономерность описания границы зоны легирования Г зависимостью R(φ). Характерное относительное отклонение от среднего радиуса приведено на рис. 2.

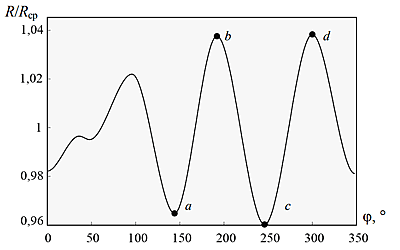
Рис. 2. Распределения отношения радиусов R(φ)/Rср на границе Г от угловой координаты, где Rср – среднее арифметическое R(φ)

 

Учитывая, что приведенная зависимость характерна для большинства исследованных стержней, методом сплайнов была построена аппроксимация R(φ), которая использовалась для моделирования технологических процессов, связанных с производством заготовок силовых стержней и оптического волокна в целом.

Отклонения геометрии легированной зоны от круговой формы могут являться причиной несимметричности полей напряжений и появления нежелательных концентраторов напряжений, что отрицательным образом сказывается на прочностных характеристиках заготовки и впоследствии на оптических параметрах готового волокна. Для численной оценки влияния данного фактора была решена краевая задача о напряженно-деформированном состоянии заготовки силового элемента анизотропного волокна типа Panda с учетом неоднородного поля температур и наличия релаксационного перехода (стеклования) при остывании заготовки из кварцевого стекла с переменным легированием оксидом бора от температур выше температуры стеклования до комнатной температуры.

1. Математическая постановка

Для определения изменения полей температур охлаждающегося волокна необходимо получить решение краевой задачи нестационарной теплопроводности, включающей дифференциальное уравнение 

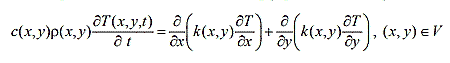
с граничными условиями

∂T(x,y,t)/∂n |_x,y∈Гн = -a (T(x,y,t)|_x,y∈Г - T_c) / k(x,y,) + εσ₀(T)⁴

и начальным условием

T(x,y,0) = T₀, (x,y,) ∈ V,

где

T – температура;
t – время;
n – внешняя нормаль к Гн;
c(x, y) – удельная теплоемкость;
ρ(,) x y – плотность;
k(x, y) – коэффициент теплопроводности неоднородного легированного материала;
Tc – температура окружающей среды;
T₀ – начальная температура;
ε – коэффициент черноты;
σ₀ – постоянная Стефана-Больцмана;
a – коэффициент теплообмена.

По найденным полям температур определяется напряженнодеформированное состояние в стержне [9]. Квазистатическая (считаем, что процесс зависит от времени, но при этом скорости настолько малы, что силами инерции можно пренебречь) краевая задача об изменении полей напряжений включает уравнения равновесия

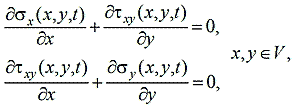
геометрические соотношения

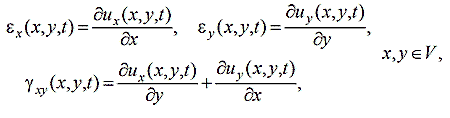
граничные условия

и физические соотношения

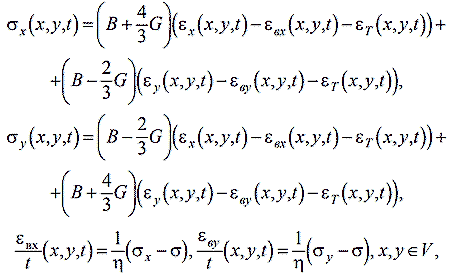
где

 

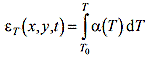
 – температурная деформация;

 

ε_вх (x,y,t); ε_{ву (x,y,t);} - – компоненты тензора вязких деформаций ˆε_в ;

σ = σkk –
среднее напряжение; Eˆ – единичный тензор второго ранга. Девиатор тензора вязкой деформации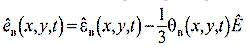 в силу того, что в расплавленном состоянии материал предполагается несжимаемой жидкостью ( θ_B = 0), равен тензору вязких деформаций ˆe_B = ˆε_B  θ_B = ε _Bkk объемная деформация; B – модуль объемного сжатия; G – модуль сдвига

 

 

Вследствие неоднородного легирования силовых стержней коэффициент линейного температурного расширения α и вязкость η являются функциями концентраций легирующих элементов и координат.

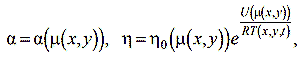
где:

U(µ(x,y)) - энергия активации;
R – универсальная газовая постоянная;
µ(x,y) – концентрация легирующих элементов в точке. 

Для численного решения задачи теплопроводности использован метод конечных элементов в традиционной реализации. Для решения задачи термомеханики избран пошаговый по времени метод [10]. Построен дискретный по времени разностный аналог краевой задачи термомеханики, соответствующий неявной схеме отыскания неизвестных на новом временном слое с итерационным уточнением на каждом шаге
величин вязких деформаций [8]. В результате на каждом шаге необходимо решать задачу линейной теории термоупругости, для чего использован метод конечных элементов.

2. Полученные результаты

Результаты свидетельствуют о том, что неоднородность геометрии ведет к существенной неоднородности и несимметричности полей напряжения. Особый интерес представляют полученные значения первых главных напряжений в центре заготовки σ1 и максимальные главные касательные напряжения τmax на границе легированной области с чистым кварцем, так как считается, что именно они могут являться причиной роста микротрещин в кварцевой заготовке.

Задача решена для нескольких возможных случаев, в каждом из которых варьировались значения функции в узлах a, b, c, d (см. рис. 2), являющиеся координатами вершин закона, описывающего распределение R(φ) на границе Г, полученного ранее, где a₀, b₀, c₀, d₀ – это исходные значение варьируемых параметров. Варьируемые параметры изменяются не больше чем на 2 % от исходного значения (таблица).

Полученные напряжения

 

Значение ∆Гτ_max, являющееся разницей между наибольшим и наименьшим τmax на границе Г, является самой чувствительной величиной к изменению геометрии сечения стержня.

 

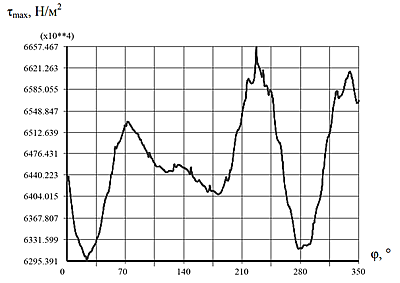
Рис. 3. Распределение максимального касательного напряжения
от угла τ_max(φ) на границе Г

 

 

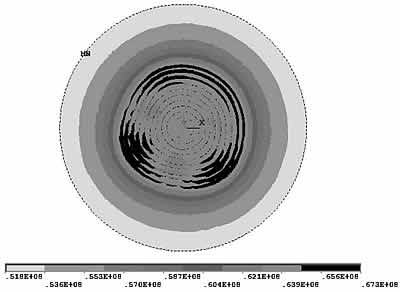
Рис. 4. Распределение напряжения τ_max(φ) в области V

Увеличение отклонения формы сечения от круга приводит к увеличению всех исследуемых величин. При незначительных изменениях геометрии сечения разница максимальных касательных напряжений на границе достигает 5–6 % и стремится к нулю, если сечение считать идеально круглым. Значения главных напряжений и максимальных интенсивностей меняется, но незначительно, в пределах 1 %.

 

Выводы

Таким образом,

• Исследовано влияние реальной геометрии формы профиля сечения заготовки легированного кварцевого силового стержня на характер поля остаточных напряжений.
• Решена краевая задача нестационарной теплопроводности и по найденному распределению температур решена краевая квазистатическая задача об остаточных напряжениях в заготовке силового стержня.
• Проведено сравнение результатов, полученных при осесимметричной постановке с идеально круглой формой сечения с результатами плоской задачи, где учитывалась реальная форма геометрии.
• Выявлено, что некруглость профиля сечения приводит к несимметричности полей остаточных напряжений по сечению, что может являться причиной разрушения заготовок.
• Наблюдаются существенные изменения величин, которые считаются важными при исследовании прочности. Разница между наименьшим и наибольшим значениями максимальных главных касательных напряжений на границе оптических сред между легированным кварцевым стеклом и чистым кварцем растет при увеличении отклонения от круглой формы сечения.

 

Библиографический список

1. Гроднев И.И., Ларин Ю.Т., Теумин И.И. Оптические кабели: конструкции, характеристики, производство и применение. – М.: Энергоатомиздат, 1991. – 264 с.
2. Волоконно-оптические датчики: пер. с япон. / Т. Окоси, К. Окамото, М. Оцу, Х. Нисихара, К. Каюма, К. Хататэ; под ред. Т. Окоси. – Л.: Энергоатомиздат, 1990. – 256 с.
3. Shelby J.E. Introduction to glass science and technology. – Second Edition // The Royal Society of Chemistry. – Cambridge, 2005. – 291 c.
4. Бурков В.Д., Иванов Г.А. Физико-технологические основы волоконно-оптической техники: учеб. пособие / Моск. гос. ун-т леса. – М., 2007. – 222 с.
5. Сметанников О.Ю., Труфанов Н.А. Технологические и остаточные напряжения в неоднородном стеклующемся цилиндрическом стержне // Механика композиционных материалов и конструкций. – 2009. – № 2. – С. 126–140. 
6. Trufanov A.N., Smetannikov O.Yu., Trufanov N.A. Numerical analysis of residual stresses in preform of stress applying part for PANDAtype polarization maintaining optical fibers // Optical Fiber Technology. – 2010. – Vol. 16, no. 3. – P. 156–161.
7. Stress birefringence analysis of polarization maintaining optical fibers / R. Guan, F. Zhu [et al.] // Optical Fiber Technology. – 2005. – No. 11. – P. 240–254. 
8. Prabhugoud M., Peters K. Finite element analysis of multi-axis strain sensitivities of bragg gratings in PM fibers // Journal of intelligent material systems and structures. – 2007. – No. 18. – P. 861–873.
9. Труфанов Н.А., Сметанников О.Ю., Труфанов А.Н. Модели формирования полей технологических и остаточных напряжений в условиях релаксационного перехода (стеклования) // Вестник Нижегород. ун-та им. Н.И. Лобачевского. – 2011. – № 4, ч. 5. – С. 2534–2536.
10. Сметанников О.Ю., Труфанов Н.А. Численный анализ технологических и остаточных напряжений в стеклующихся телах // Вычислительная механика сплошных сред. – 2008. – Т. 1, № 1. – С. 92–108.

You have no rights to post comments